1)ヨーロッパ主要国での終焉時期:
新型コロナ肺炎に蹂躙された感じの欧州各国であったが、その先が見えてきたような気がする。欧州では、国境がないに等しく、例えばドイツが克服しても、イタリアやフランスから感染者が徐々にでも流入すれば、なかなかその終焉が見えないだろう。
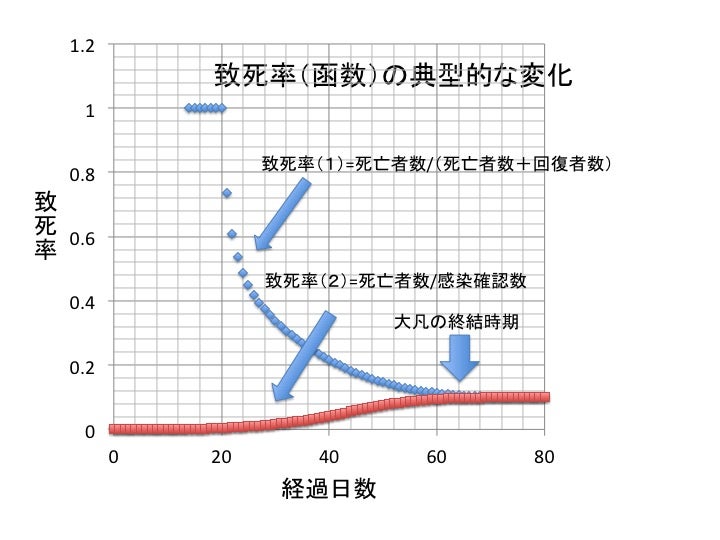
そこで、スペイン、フランス、イタリア、ドイツ、スイスの主要5カ国の合計で、コロナ肺炎の致死率の図示を、今までと同じ手法で行ってみた。ここで致死率と言うのは、以下のように定義した時間の函数であり、この病気の定数としての致死率ではない。結果を下に示す。
致死率(1)は死亡者数/(回復者数+死亡者数)であり青い点で、致死率(2)は死亡者数/感染確認者数であり赤い点で、それぞれ示されている。
致死率(1)と致死率(2)は、最終的に一致するので、このグラフ上で2つの曲線が一致する点を予想できれば、その横軸の値が感染終結のおよその時期と考える事ができる。この図では、5月中旬あたりが、終結時期として予想される。
従って、経済活動などの復活が議論され始める時期かと思う。中程度の被害で何とかおさまりそうなのは、厳しい都市封鎖、多数のPCR検査で探しだした陽性者の強制或いは自己隔離の結果だろう。
2)コロナ肺炎との各国の戦いの差について、
この肺炎ウイルスとの戦いでは、政府と一般国民の両方が団結して、努力しないと最小限の被害で抑え込むのは難しいだろう。その理想に近い戦いを行ったのは、この5カ国ではドイツとスイスのようである。それと比較して、イタリア、フランス、スペインは、かなり大きな被害を出した。
この点を少し考えるために、以前紹介したモデルでの致死率(1)&(2)の時間変化との比較を行ってみる。ここでは、患者の発生を単純に初等函数で置き換えている。従って、本当のところは、シミュレーションという程の計算ではない。https://ameblo.jp/polymorph86/entry-12587988007.html
モデル計算の詳細を書くと:感染して、二週間後に全て発病し、一週間後に10%の人が死亡する。生き残る人は、更にもう一週間後に検査を経て退院するというモデルである。患者の発生は誤差関数と仮定した。
P=aEXP{-(x-b)^2/2c^2}
ここでbは感染者数が最大になる日、cは患者発生の偏差である。bとして、30(日)、cとして10(日)を用いた。EXPは指数函数を、^2は2乗を表す。
下にドイツとイタリアのグラフを示した。
ドイツのケースでは、致死率(1)と致死率(2)の変化は前図とよく似ている。ドイツでは、最初、死者が出るなどして病気の発生に驚き、急いで患者数の把握を開始する。その時、回復者は少ないので、非常に高い致死率(1)が出る。患者は直ぐに大勢見つかるので、致死率(2)は低い値になる。治療に実績が出始めると、元々の致死率(病気本来の定数)がそれ程高くないので、致死率(1)は急激に低下する。
フランスもイタリアと殆ど同じだが、もう少しガタガタした曲線になった。両国では、検出した発病者全員に西欧社会の最新の治療が施せなかったのではないだろうか。つまり、一部医療崩壊が起こっていたのではないだろうか。そのように考えざるを得ない。
隣同志なのにこのような大きな差がでるのか? 日本でも議論されているように、PCR検査で発病者を能率良く検出しても、病院の治療体制がしっかりしていなければ、逆に多数の死者を出してしまうのだろう。
(16:05文章を全面的に修正しました。失礼しました。)


0 件のコメント:
コメントを投稿